タイヤの役割と特性
私の父が子供のころの絵本に、将来の夢の乗り物として空飛ぶ自動車が描かれていたそうだが、私が子供の頃の絵本にも同様な記載があった。私の息子が読んだ絵本やアニメにも、夢の乗り物として空飛ぶ自動車が描かれていた。これだけ長い間空飛ぶ自動車が夢とされて来たにもかかわらず、なぜ未だに夢なのだろうか。これまでには、ホバークラフトとよばれるタイヤを使用しない乗り物も作られているし、垂直離陸のできる小型ヘリコプター等が自動車のように使用されると期待された時もあった。さらに、最近は空飛ぶ自動車がドローン技術をベースにイメージできるようになってきたが、世の中の流れがそちらになかなか移行しないのは何故だろうか? また、30〜40年後には多くの自動車が空を飛んでいるのだろうか? 一部にはそのような乗り物が出て来ている可能性はあるものの、多分この答えはNo!であろう。

なぜ自動車が空を飛ぶことが夢のままなのだろうか?
なぜ自動車が空を飛ぶことが夢のままなのだろうか?
安全性の観点から航空管制等の整備の必要性もあるが、ひとつの大きな問題は力の発生機構にあると考えている。ここで、旋回時内側に発生する求心力(旋回を維持するための力)を自動車と飛行機で比較してみる。飛行機の翼や自動車のタイヤに発生する力を図1に示す。翼が進行方向に対し迎角αを持つと、翼には図に示す揚力が発生し、その特性は迎角の関数として表される。タイヤも同様であり、進行方向に対し迎角(タイヤの場合は横すべり角と呼ぶ)を生じると、翼と同様タイヤにも直角方向の力が発生する。その特性は飛行機の翼と同様、迎角(横すべり角)の関数として表される。これが乗り物の旋回時の求心力となり、外側にその慣性力である遠心力が発生する。
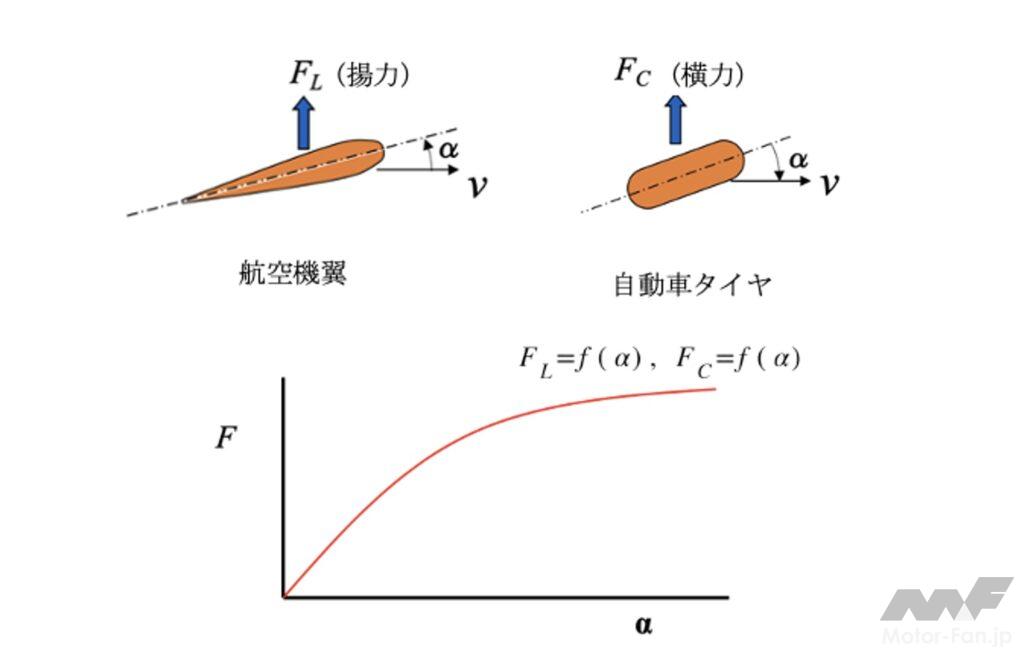
翼の場合、ロールにより重力をささえる成分と求心力となる成分を考える必要があるが、ここでは単純に求心力成分と旋回の関係を考える。半径Rの円弧上を旋回する場合、これらの乗り物の遠心力はmv2/Rで与えられるため、同一半径を通過する場合、速度が2倍になれば求心力を4倍にする必要がある。翼の場合、この力は次式で示される。

ここで、ρが空気密度であり、sが投影面積、CLが形状係数、vが速度となる。そこで、航空機の場合、同一半径を飛行中、速度を2倍にすると発生する力は4倍となる。つまり、同一半径、同一迎角を維持して速度を増加させことで必要な求心力を発生することができ、機体の姿勢を変えないで高い速度の旋回が可能となる。このため、一部航空機では10Gを超える旋回が可能となる。そこで、旋回中速度を増加させても姿勢変化無しで必要な求心力を得ることができるため、高速飛行に向いた力の発生機構を持っていることになる。逆に速度が低くなると揚力を確保することができず飛行を続けられなくなるため、タイヤを用いた地上走行をする必要がある。さらに、横風等に大きな影響をうけるため、風が強い状態での安定した飛行を維持することが非常に難しい。航空機の場合、自機から半径150m内に、また高度差が60m以内に他の航空機が入ってくるとFAAではニアミスと定義し、安全上の大きな問題としている。これは力の発生機構上、その程度の距離ではすぐに風等にながされ衝突する可能性があることを意味し、近接した飛行が非常に危険であることを示している。ブルーインパルス等による近接飛行がショーとなり得るのは、そのような飛行が極端に難しいためである。

これに対し自動車のタイヤ力は摩擦により発生するため、概ね速度に関係なく力が発生する反面、同一半径の旋回で速度を2倍にした場合横すべり角を約4倍にする必要があり、大きな車両の姿勢変化をともなうことになる。特に力発生のもととなるタイヤと路面間の摩擦係数は最大で概ね1程度であるため、特殊な車両の場合を除き理想状態であっても1G程度の旋回が限界となる。しかし、この摩擦係数の範囲内では速度に関係なく安定した制動力や横力を発生させられるため、制動時停止するまで大きな制動力を維持することができる。そこで、自動車は高速の旋回には向かない反面、他の車両との車間距離をつめた追従走行や併走を可能とし、さらに横風の中での過密運行をも可能としている。このように、高速道路を含め一般道における自動車の過密走行が可能なのは、タイヤ力の発生機構に由来していると言っても過言ではない。
次回は、タイヤ力がどうして発生するか、そのメカニズムに注目する。












