目次
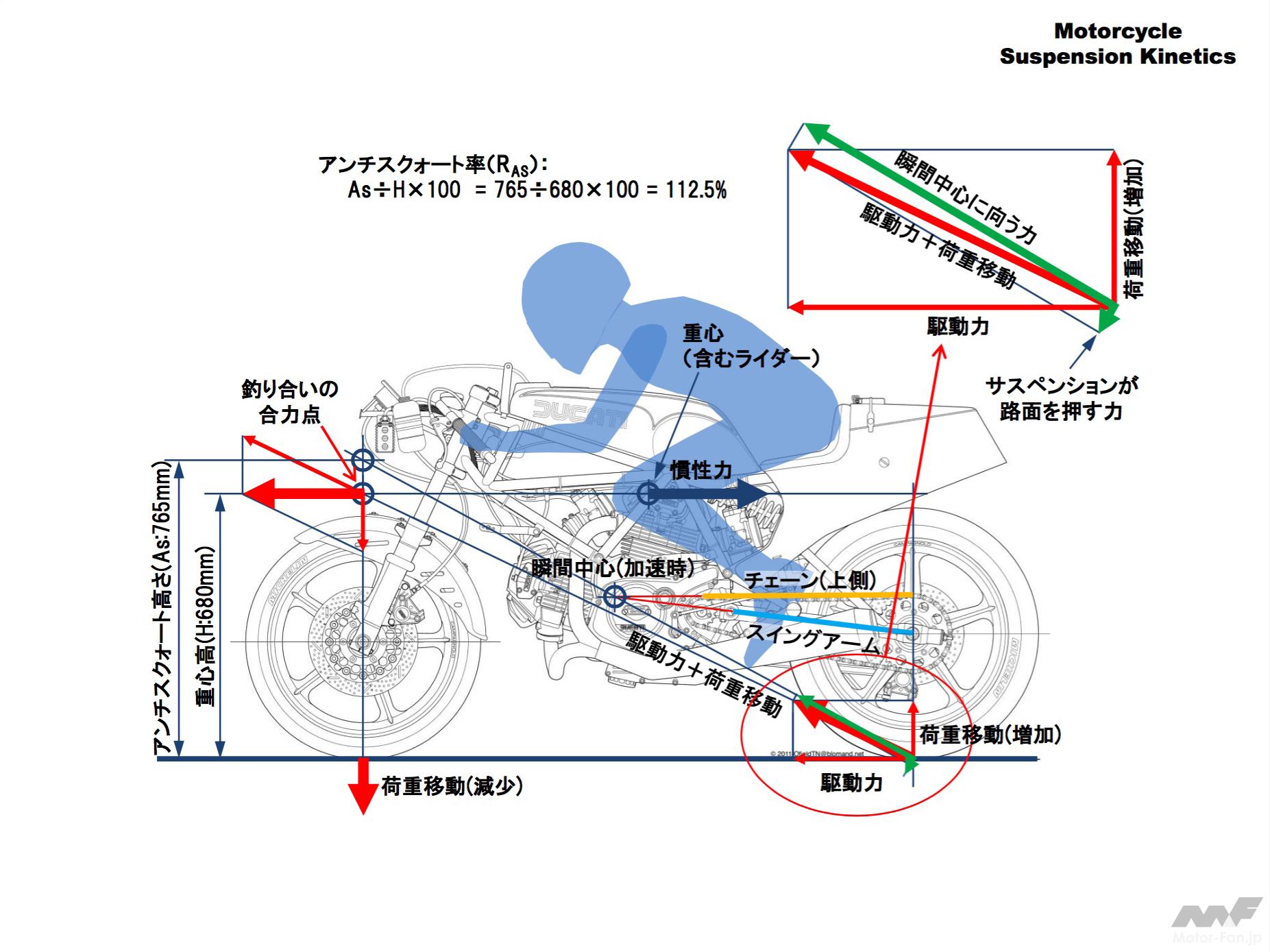
加速時の姿勢変化
加速時の姿勢変化、特にリヤは沈むのか沈まないのか、沈まない理由はスイングアームの角度なのか、ドライブ／ドリブンチェーンスプロケットとスイングアームピボットがつくる三角形なのか…いやシャシーダイナモで駆動力をかけたらリヤは沈んだぞ！等々怪しい都市伝説の宝庫でした。
これから述べることは個人の見解でも、仮説でもなく、ちゃんとした物理法則と機構学から導かれるものです。
加速時のリヤサスペンションの動き
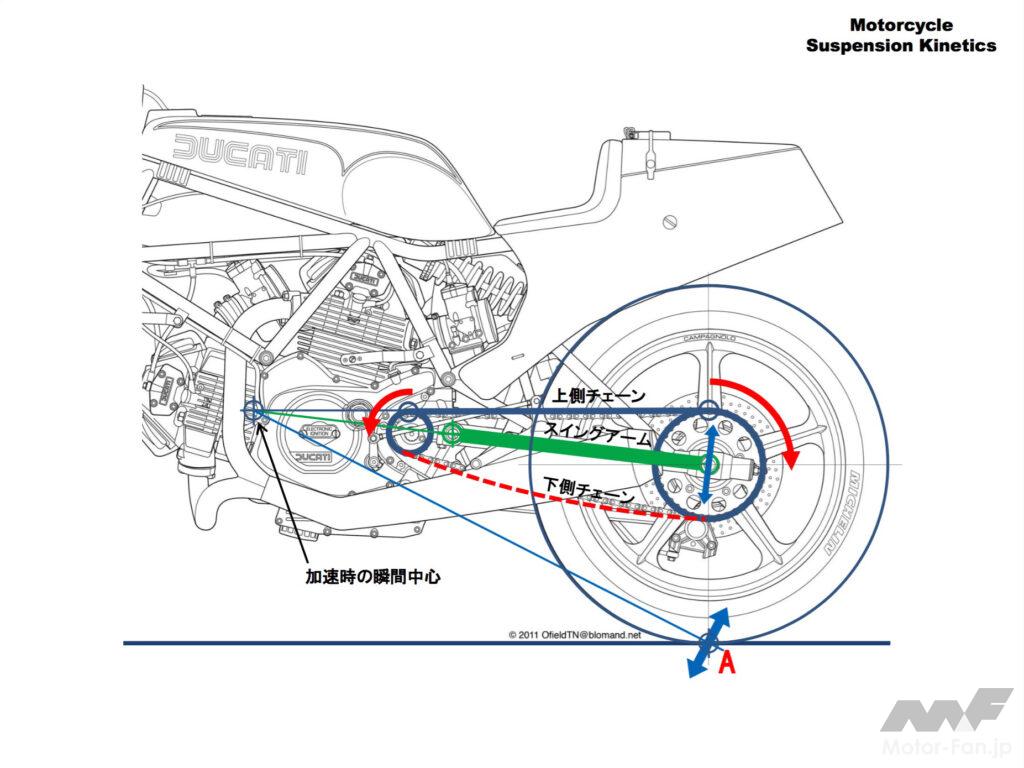
MCが加速する時のタイヤの接地点（A）の動きを考えます。
実際にはタイヤは回転しているのですが、加速方向に力を加えた状態でタイヤは回転しない場合を考えてみてください。
このとき、加速時には上側のチェーンはピンと張って力を伝え、下側のチェーンはたるんで力を伝えません。この上側チェーンをピンと張った状態でタイヤの接地点（A点）を動かしてみましょう。
スイングアームは車体のピボットを中心にリヤハブ（タイヤではない）を回転させます。そしてこの時上側チェーンはふたつのスプロケットに沿って向きを変えます。
ピンと張られたチェーンはサスペンションアーム（リンク）と同じように動きます。このチェーンとスプロケットの動きが接地点の上下動に連れてタイヤとホイールをハブの回りに少し回転させます。
このスイングアームと上側チェーンの動きは合成され結果的にタイヤとホイールはそれぞれの延長線が交わる点のまわりに回転しようとします。
この点を「加速時の瞬間中心」と呼び、サスペンションの上下の動きの中心になるとともにサスペンションと車体が力をやり取りする力の合力点にもなります。
加速時のリヤサスペンションはダブルウィッシュボーン！
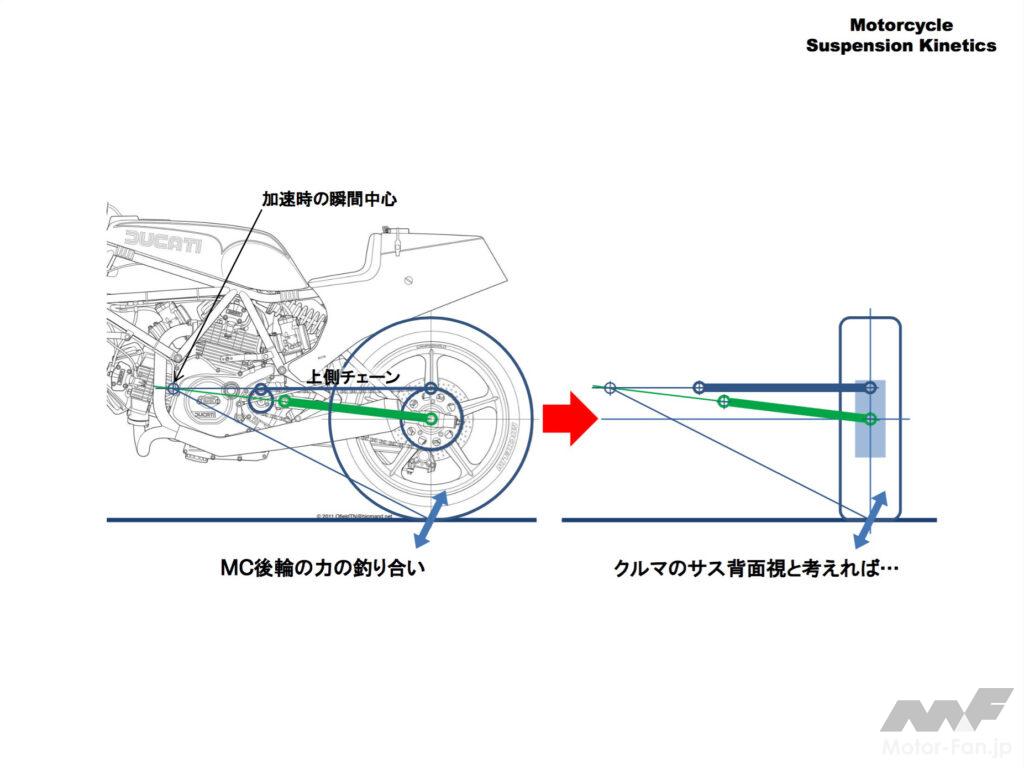
リヤサスペンションの接地点の動きと力の釣り合いは図のようにスイングアームと上側チェーンで規制されて動きますが、この動きはクルマのダブルウィッシュボーンサスペンションと似ています。
極限すればタイヤが丸く見えるか四角く見えるかの違いです。
「チェーンはリンクである」ということが理解できればMCのサスペンションを理解する入口に到達できたといえます。
加速時にリヤサスペンションにはたらく力
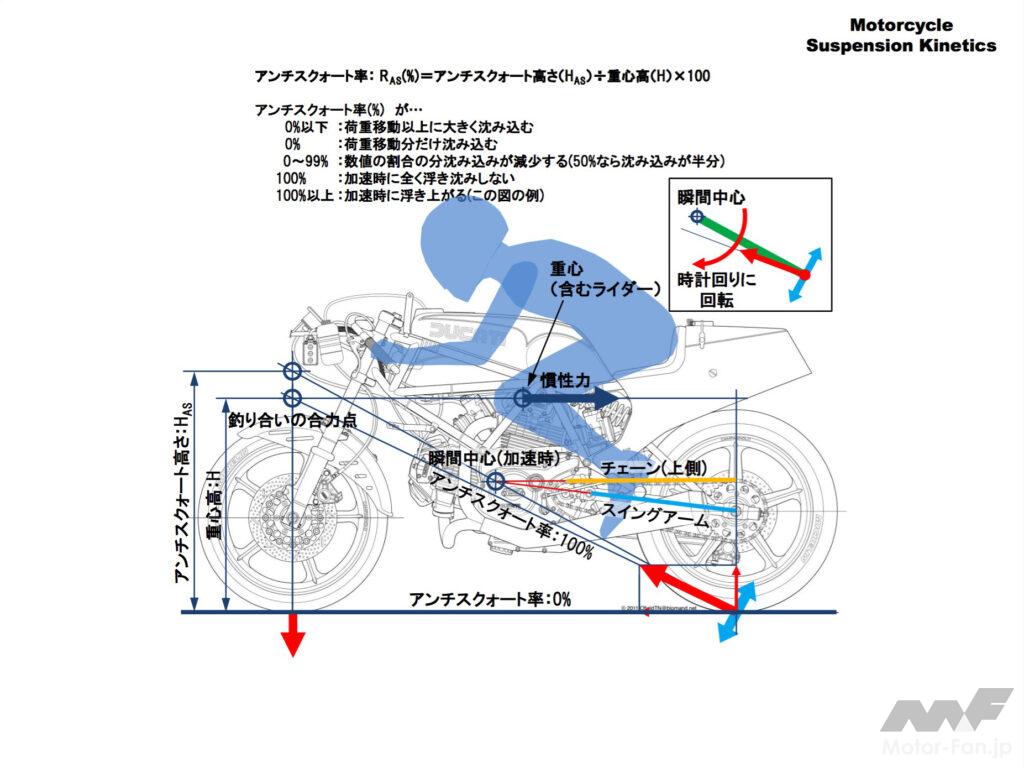
この図は加速時の力の釣り合いと後輪接地点の動きを重ねて描いたものです。
注目点は後輪接地点の釣り合いの合力点に向かう赤いベクトル（矢印） と瞬間中心の向きとがわずかにズレていることです。
瞬間中心の方向が後輪接地点の赤いベクトルよりわずかに上を向いています。後輪接地点の回転の中心より後輪接地点に加わる力の方向が下を向いているのでリヤサスペンションはこの図で時計回り、サスペンションが伸びる方向に動こうとします。
アンチスクォート効果というのは荷重移動に逆らってサスペンションが縮むのを抑える効果のことです。
この図のように瞬間中心が力の釣り合いの合力点の方向より、さらに上にあるとサスペンションは伸びてアンチスクォート率は100%以上となります。
アンチスクォート率が100%を超えると、後輪は荷重移動に逆らって路面を押し、サスペンションが伸びて車体後部を持上げます。
もし、力の釣り合い点の方向と後輪接地点の瞬間中心が一致していたら。サスペンションは伸びも縮みもしなくなります。この状態がアンチスクォート率100%です。
瞬間中心が路面にあればアンチスクォート率が0%となり荷重移動に応じてリヤサスペンションは縮みます。瞬間中心がアンチスクォート率0%と100%の間にあれば、その割合に応じてリヤサスペンションの縮み量が低減されます。
アンチスクォート率は以下の式で計算できます。
アンチスクォート高さ（HAS）は後輪接地点と瞬間中心を結ぶ線を前輪の真上まで延長したところの高さです。
アンチスクォート率： RAS（%）＝アンチスクォート高さ（HAS）÷重心高（H）×100
アンチスクォート高さとアンチスクォート率
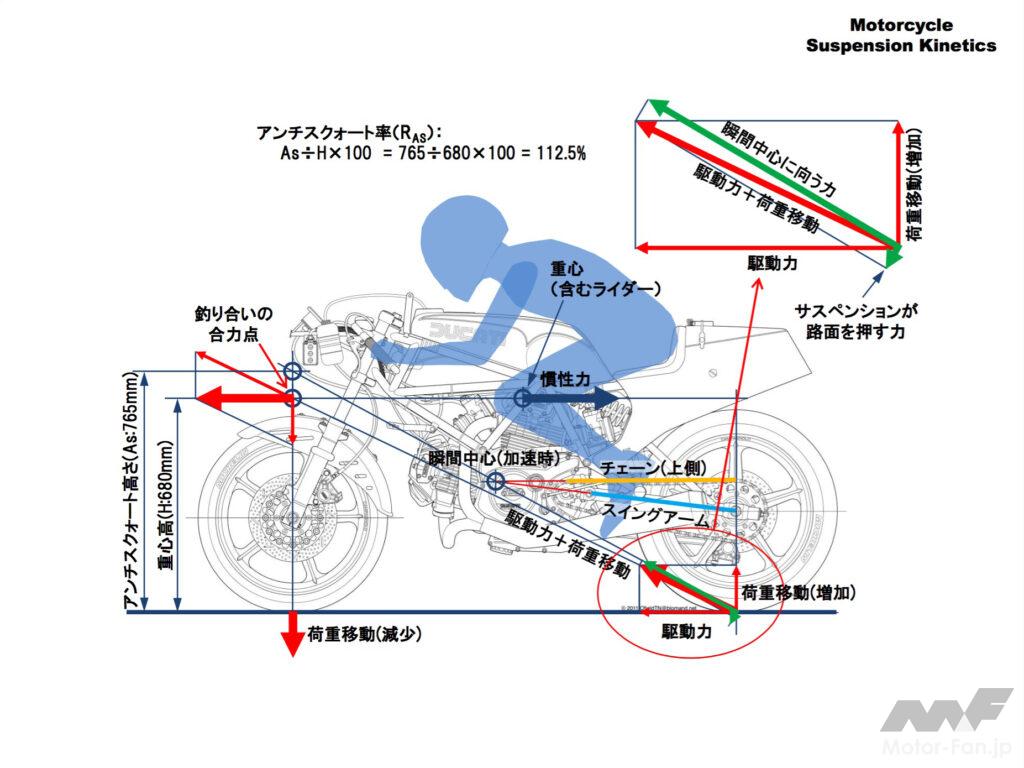
前の図をこの例に沿って詳しくみていきます。
釣り合いの合力点はホイールベースと重心高だけで決まるので、そこに向かうベクトルの向きはサスペンション形式やセッティングとは無関係で一定です。
いっぽうサスペンションはそれと切り離して自由に設定できます。
この図のサスペンションはアンチスクォート率が112.5%となっており、荷重移動の12.5%に相当する分サスペンションが逆に伸びます。
右上の接地点のベクトル拡大図のサスペンションが路面を押す力（短い緑のベクトル）が、荷重移動（増加）のベクトルの12.5%だということです。
拡大図で駆動力＋荷重移動（赤の太い矢印）をそのままにして、瞬間中心に向かう力（緑の太い矢印）の方向を変化させて作図するとアンチスクォートの力の大きさがわかります。
しかしベクトルの合力を作図するより、前の図の方法でアンチスクォート高さ（As）からアンチスクォート率を作図をして求めたほうが簡単です。
インターネットにあるMCの側面の画像やご自身のMCを側面から観察し、目分量でアンチスクォート率を推測してみるのも面白いです。大抵は100%前後にあるのがわかります。これは荷重移動を速やかに終了させ後輪のトラクションを稼ぐための設定です。
いっぽう前輪はアンチスクォート効果とは無関係なので荷重移動の分だけフロントサスが伸びて車体の前部が持ち上がります。結果として車体が前上がりになるので「リヤが沈み込んでる」と勘違いしている人もおられるようです。
もし、皆さんのMCがスイングアームとチェーンではなくBMWのパラレバー式以前のシャフトドライブだったり、スクーターのようなユニットスイング式（パワートレインがサスと一体）だった場合は瞬間中心＝スイングアームピボットとなるのですが詳しくは別途解説します。
MCのリヤサスペンションはリンク機構のおもちゃ箱だ！
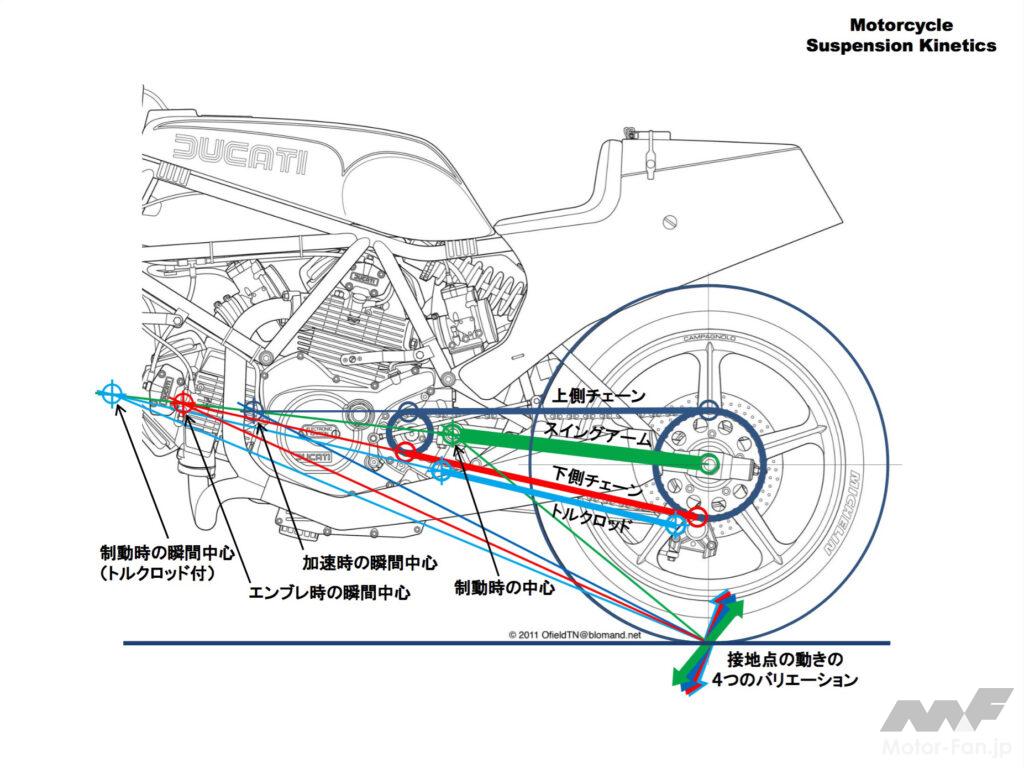
加速時の瞬間中心はスイングアームと張っている上側チェーンの延長線の交点で決まります。
エンジンブレーキ時はスイングアームと張っている下側チェーン（エンブレ時は下側チェーンが張る）の延長線の交点で瞬間中心が決まります。
制動時はブレーキキャリパーがスイングアームに固定されチェーンは上下とも弛んでいてキャリパーがスイングアームにトルクを伝えるのでいるのでスイングアームピボットがそのまま回転の中心になります。
さらにトルクロッドを使ったブレーキの場合はトルクロッドとスイングアームの延長線の交点が瞬間中心になります。
MCはスロットルの開け閉め、ブレーキのオンオフで瞬間中心が目まぐるしく変ります。これがクルマにはないMCのリヤサスペンションの最大の特徴です。
瞬間中心が異なると接地点の動きも変わります。それによってサスペンションの特性が変わってしまいますが、逆にその違いを積極的に利用することもできるわけです。