著者自己紹介 J.J.Kinetickler (J.J.キネティクラー) 日本国籍の機械工学エンジニア。 長らくカーメーカー開発部門に在籍し、ボディー設計、サスペンション設計、車両企画部門を経験。 退職後、モデルベース開発会社顧問を経て、現在は精密農業関連ベンチャー企業の技術顧問。 「物理を超える技術はない」を信条に、読者に技術をわかりやすく伝えます。
ウィリーとジャックナイフ
この講座はいきなり「ウィリーとジャックナイフ」という限界の状態から始まります。限界の状態を理解することによって、MCの車体パッケージ(レイアウトの考え方)が見えてくるからです。
はじめの一歩はベクトルから
まず、これからの解説のもとになっている「ベクトル(vector)」の基本です。ほんの少し我慢してお付き合いください。
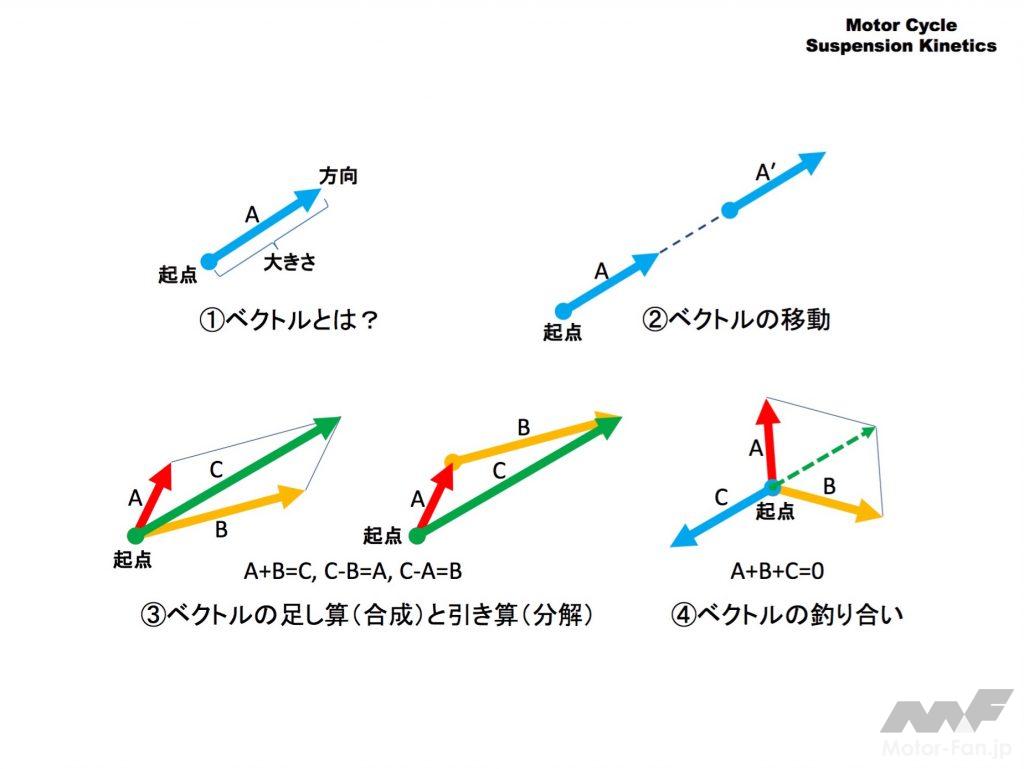
「ベクトル」とは「大きさと方向を持つ量」のことで色々な物理量を表現できます。例えば「北東に3km」というのも立派なベクトルです。ここでは力や速度、加速度に対して使います。
以下はベクトルの理解のための最小限のお約束です。
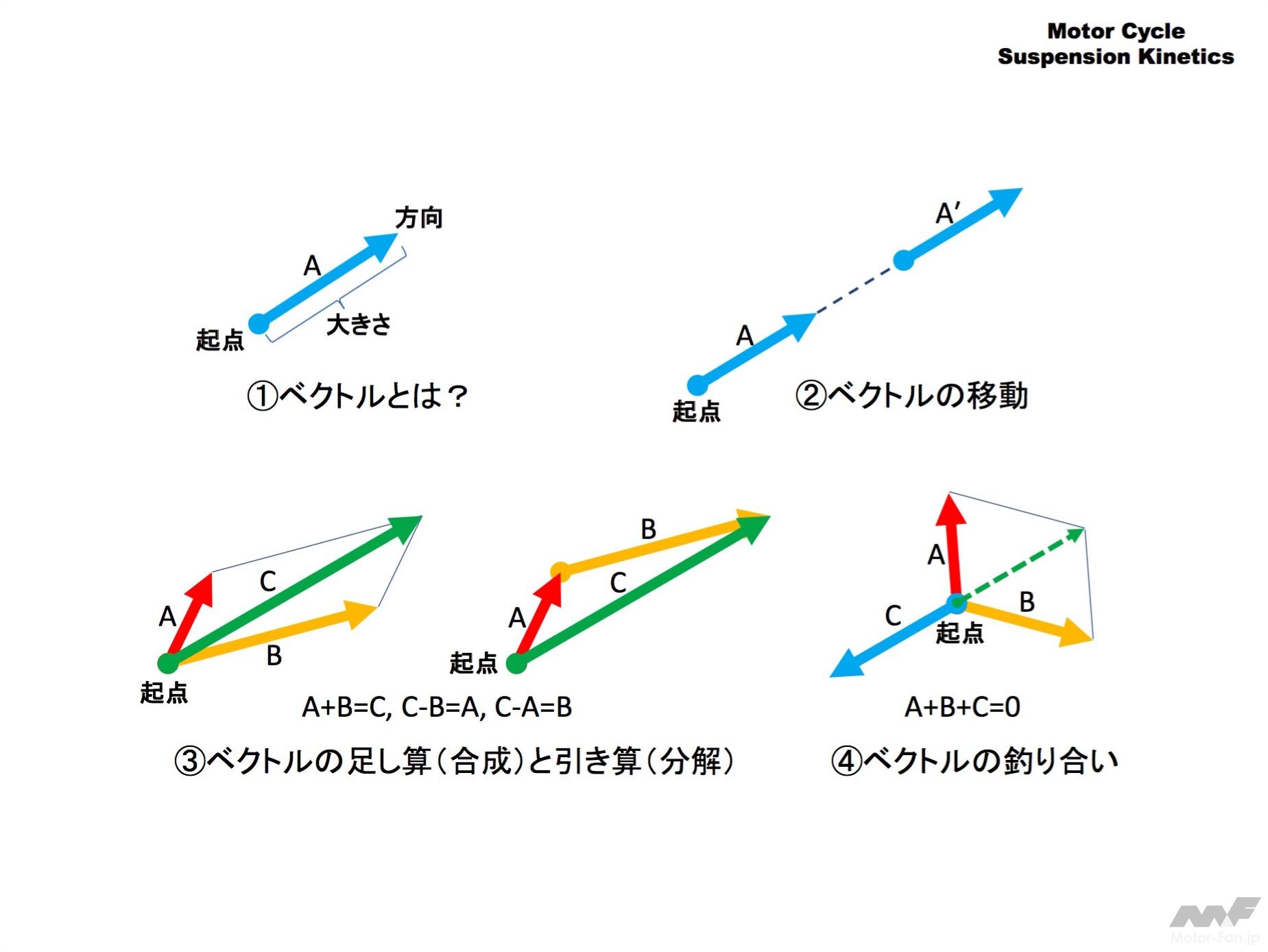
① ベクトルは矢印の起点(始点)で作用する位置を、向きで方向を、長さで量を表現します。
② ベクトルはその作用する方向には自由に移動できます。
③ 2つ以上のベクトルは起点が同じ、または2の移動で起点が一致できるなら、足し算や引き算をすることができます。
左のように平行四辺形を使って表現するのが基本です。
元の起点が同じであれば右のように矢印を移動させ起点と先端を重ねて足し算を表現することも可能です。
④ ベクトルA,B,Cの足し算が「ゼロ」になるとき3つのベクトルが釣り合っていると表現します。解説中ではその起点を「釣り合いの合力点」と表現しています。
これは起点を結び目にして3方向にロープを伸ばし、矢印の大きさの比率で綱引きするのをイメージしていただくとわかりやすいです。
入力と反力
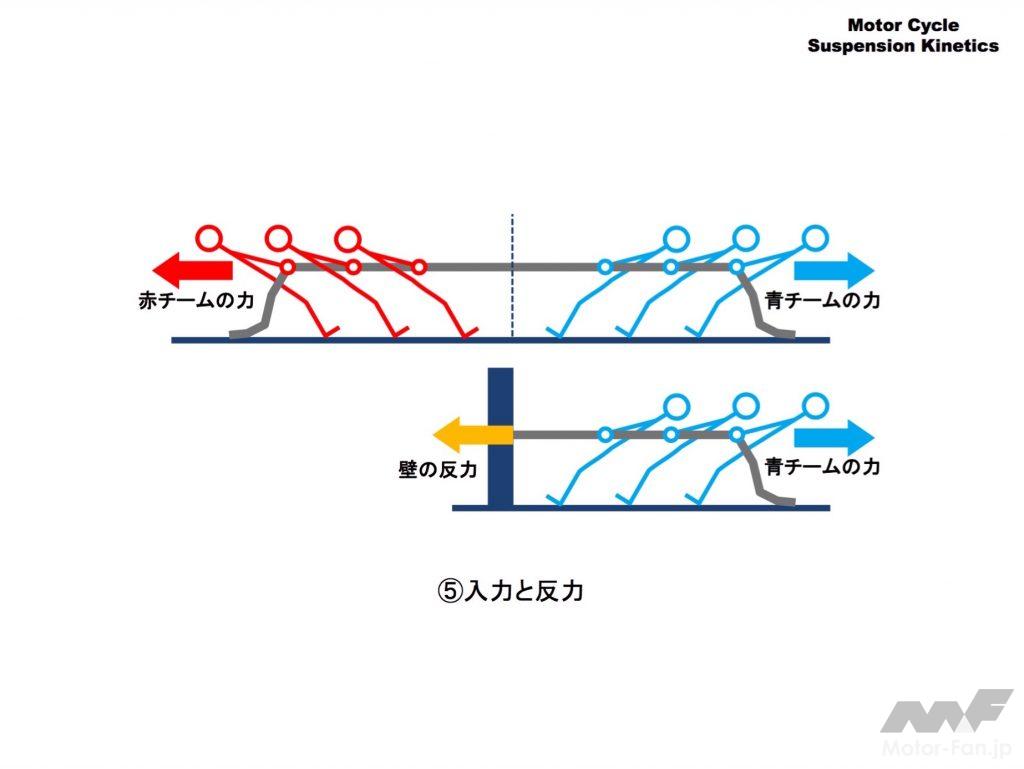
次に、この解説でたびたび登場する「反力」です。
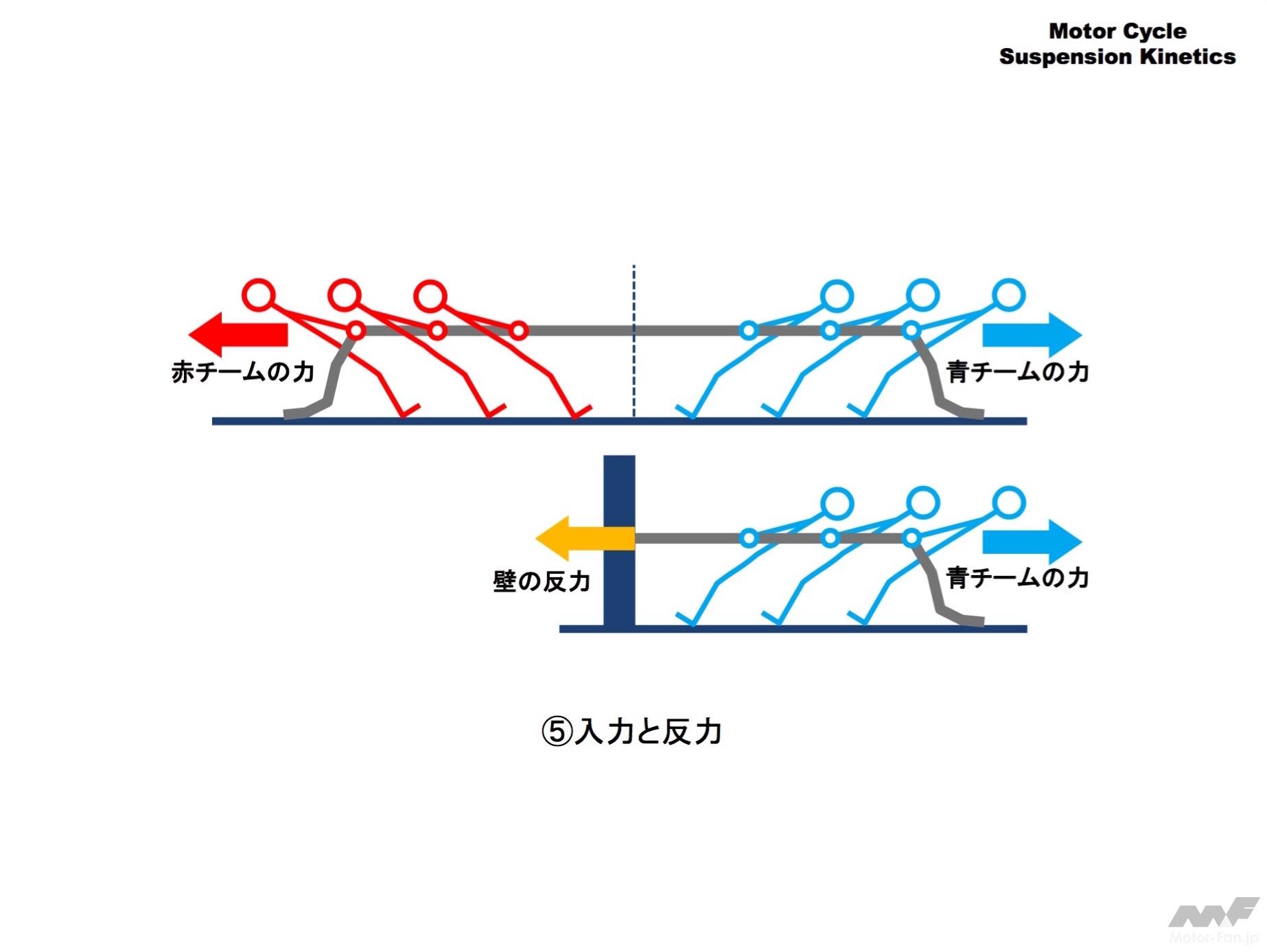
上の図は綱引きの絵です。青チームと赤チームが綱を引き合って一歩も譲らない状態です。この時、青チームが綱をゆるめると赤チームは後退し綱引きに勝利します。
下の図は壁のフックに綱を結んで青チームが綱を引きます。この状態では綱は全く動きません。
この状態は青チームが綱を引いた力と向きが逆で常に同じ力で壁が引き戻していると考えます。これを壁の「反力」といいます。
この状態は青・赤チームの綱引きとよく似ていますが、青チームが綱をゆるめても何も起こりません。引張る力をゆるめると反力も小さくなるからです。この点が綱引きと違うところです。
力が釣り合っている時、必ず「入力」と「反力」が生じています。
ようやくMCにたどり着きました
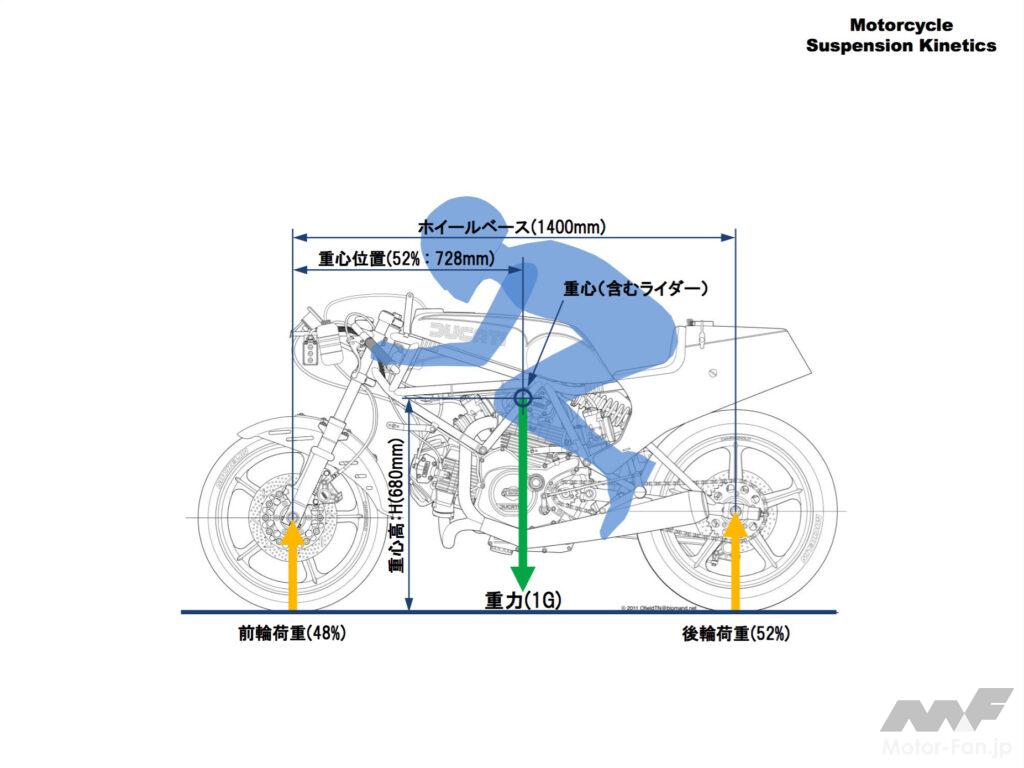
MCの静止時の力の釣り合いをベクトルで表現します。
重心に重力(地球とMCが引き合う力)がはたらき、前後輪に重心の前後位置(配分)にしたがって接地点に路面反力(路面がMCを押し返す力))゙生じます。
「地上に静止している」という状態をこの「3つの力が上下方向に釣り合っている」というように考えます。
簡単なことをわざと難しく表現しているようですが、この考え方が基本で大切です。
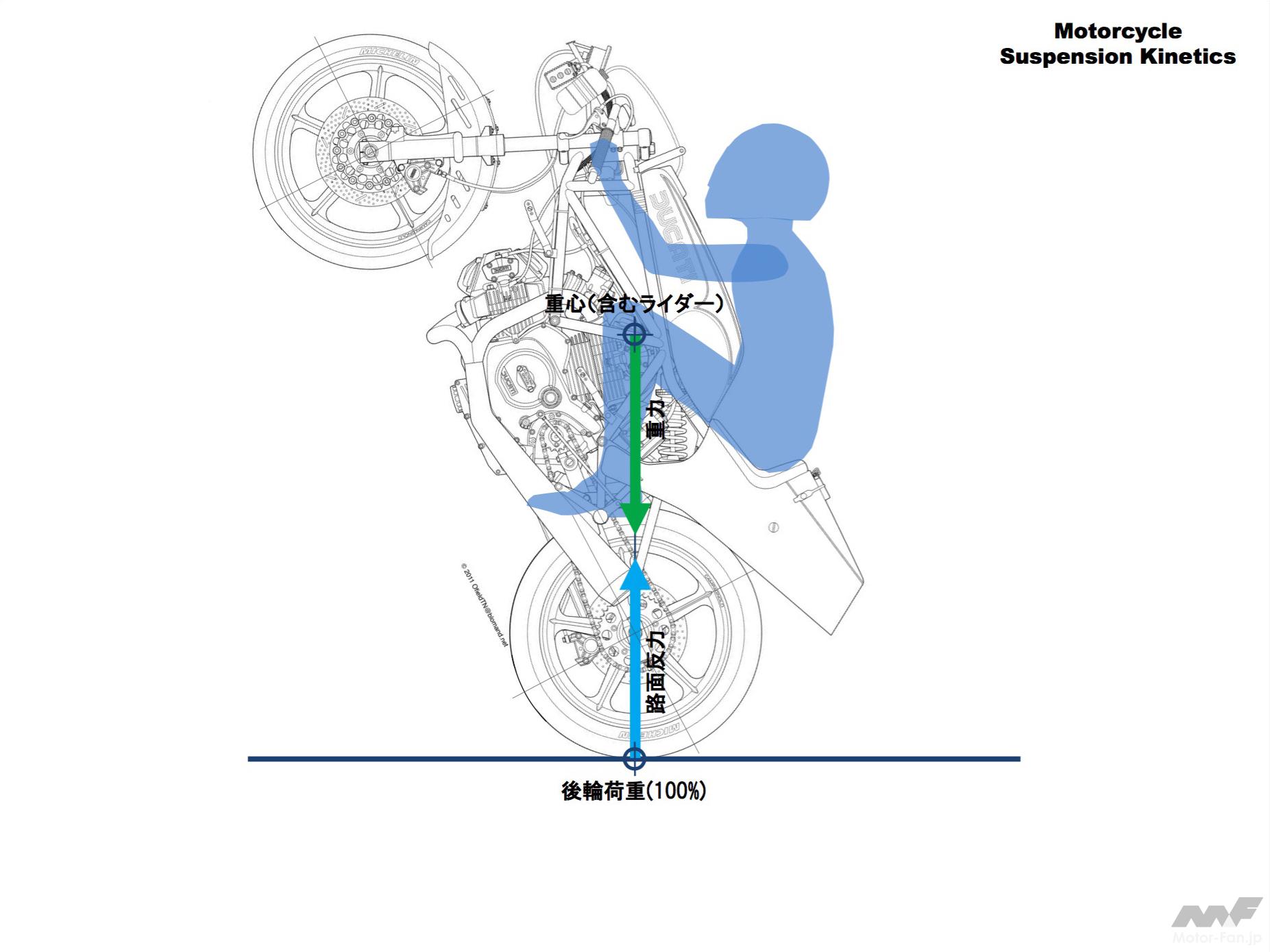
MCのウィリー
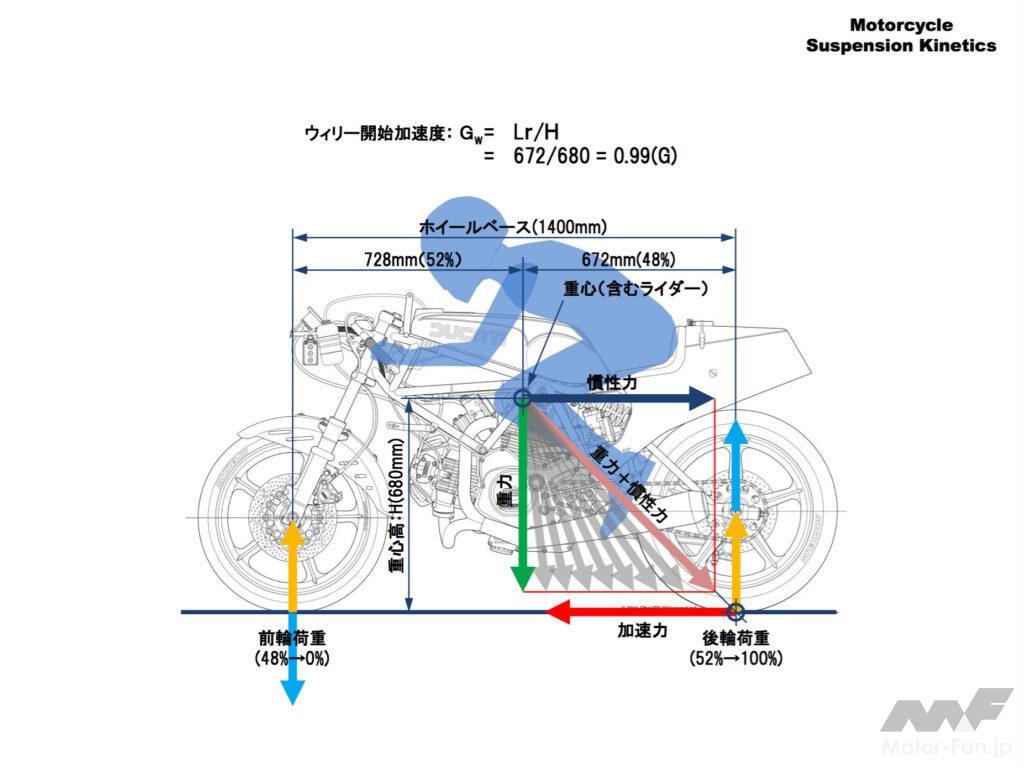
ウィリーは重力も加味して考える必要があります。
それでは先程の静止状態から加速してみましょう。
加速すると後輪の接地点に加速力が加えられ、重心には逆向きの「慣性力」(物体がそこに留まろうとする力)という反力がはたらきます。加速力と慣性力は向きが逆、重心の高さ分だけ上下に位置がずれているので、それと釣り合うように接地反力が変わります。具体的には後輪の接地反力が増加し、前輪の接地反力はその分減少します。これは前輪から後輪に荷重が移るとみなせるので「荷重移動」と呼びます。
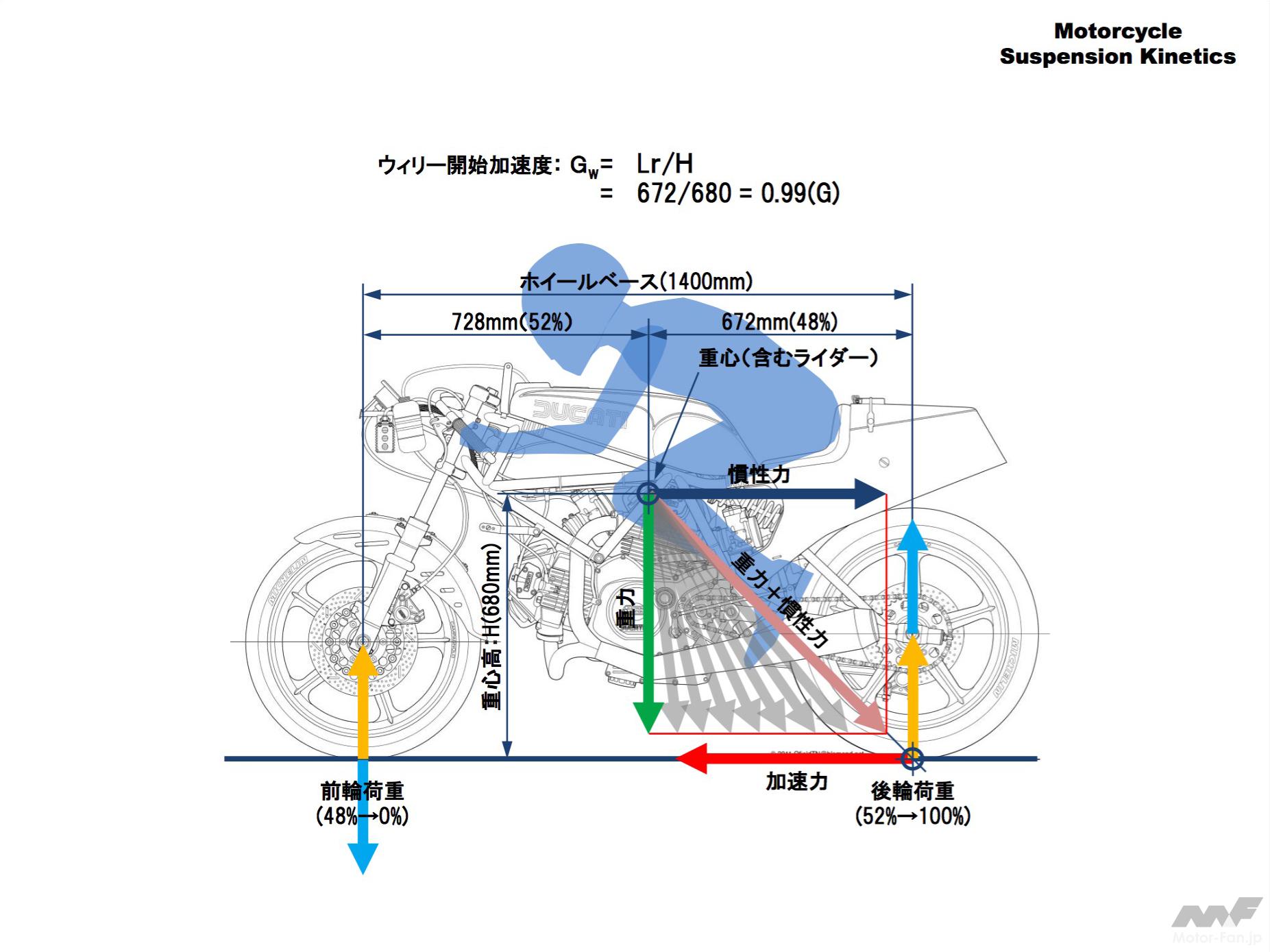
加速度をどんどん大きくしていくと前輪から後輪に荷重が移動し、前輪荷重がついにゼロ(路面反力-荷重移動=0)になります。この状態から更に加速度を上げると前輪が持ち上がり転倒します。この状態で転倒しないように前輪を持ち上げた状態でバランスをとって走り続けるのがウィリーです。
この状態は重力と慣性力の足し算ベクトル(ピンクの矢印)の方向が後輪接地点を向いているということです。これからわかるようにウィリー開始加速度が低い(簡単にウィリーしてしまう)条件は重心が高く、また後方にあることです。ちょっと考えればあたりまえですね!
ウィリーが始まる加速度を「ウィリー開始加速度(Gw) *1」とすると次の式で計算できます。
ウィリー開始加速度(Gw)=重心から後輪までの水平距離(mm)÷重心高(mm)
*1:加速度の単位はm/s2なのですが、ここでは特にことわらない場合は加速度を重力加速度(9.81m/s2)で割った値(G)であらわします。Gであらわした方が耳慣れていて直感的にもわかりやすいからです。たとえば4.9m/s2で加速するというより「0.5Gで加速する」という方がわかりやすいと思います。
ウィリーを維持するには
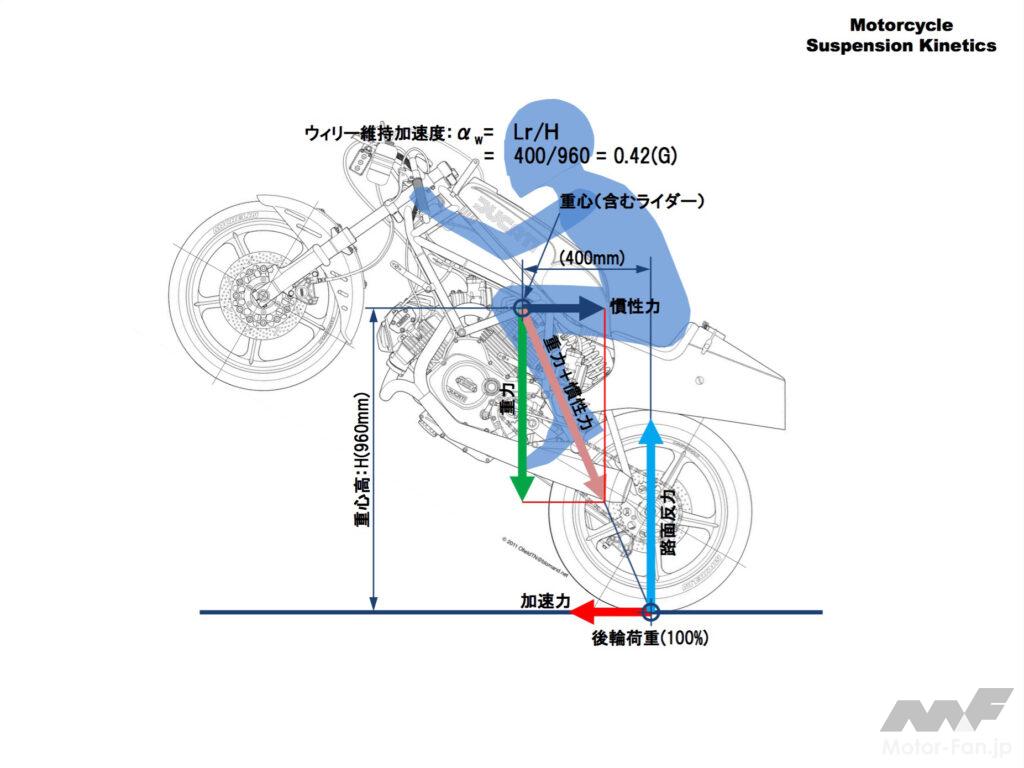
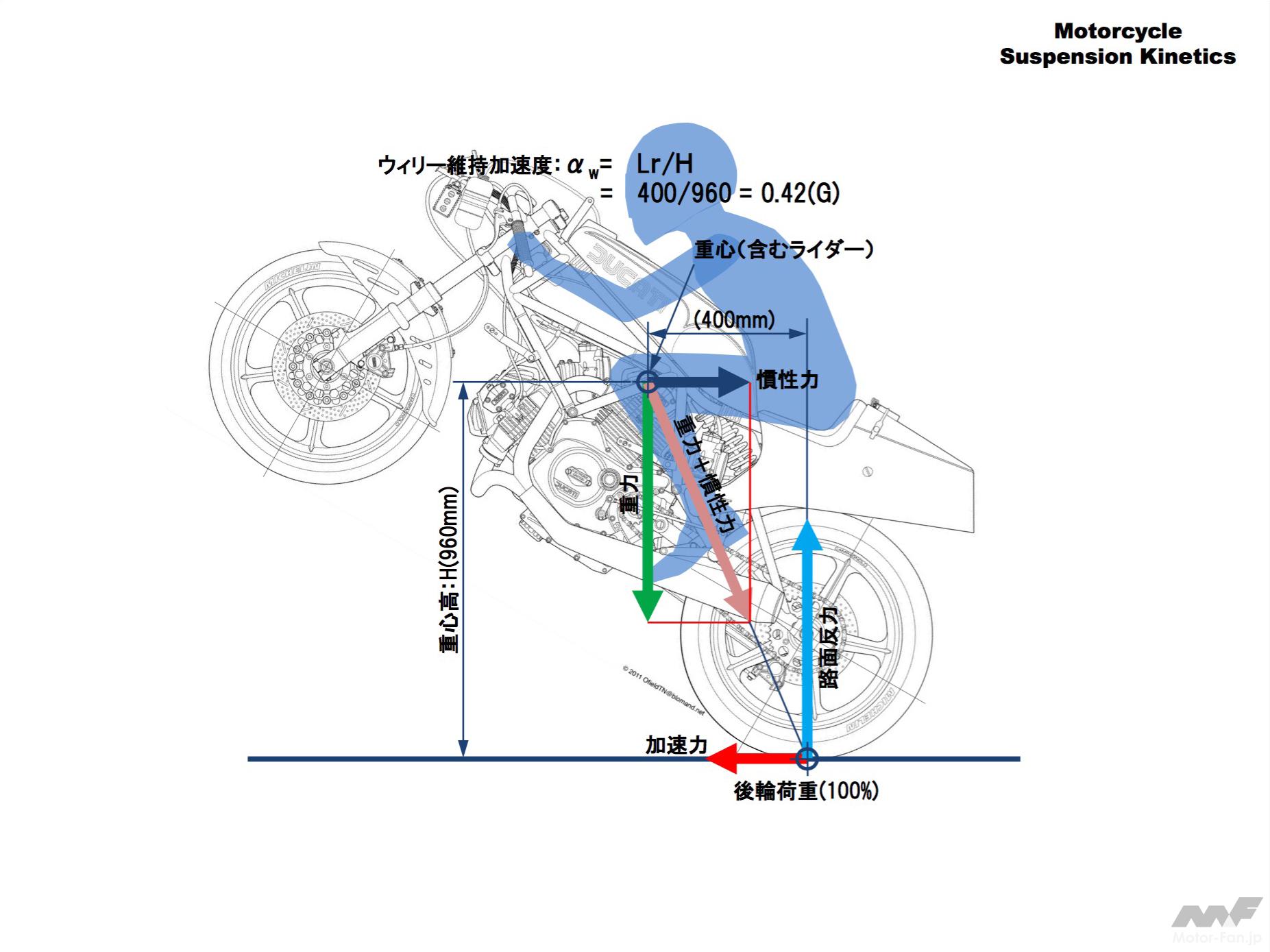
一旦前輪が持ち上がると更に重心高が上がり後方にも移動するのでウィリーを維持するための加速度の値が小さくなります。
この加速度をスロットル(と場合によってはブレーキ)でコントロールするとウィリーの姿勢を保ったまま加速できます。
この図の場合0.42Gの加速度でウィリーを続けられます。
MCの曲乗り
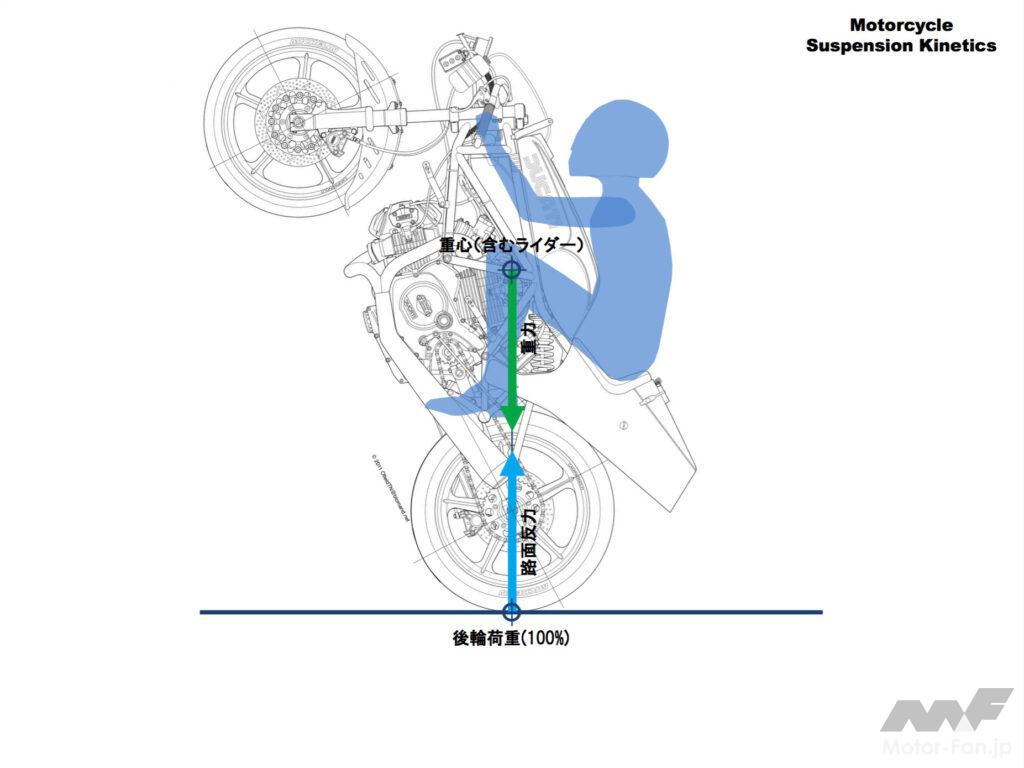
どんどんと前輪を高く持上げ、最終的に重心が後輪の真上にくると、今度は前輪を持上げたまま加速度ゼロの一定速度でバランスをとって走行することができます。
いわゆる「曲乗り」の状態ですね。この状態では姿勢維持にスロットルとリヤブレーキの両方(時には体重移動も!)を使う必要があります。
こんどはジャックナイフ
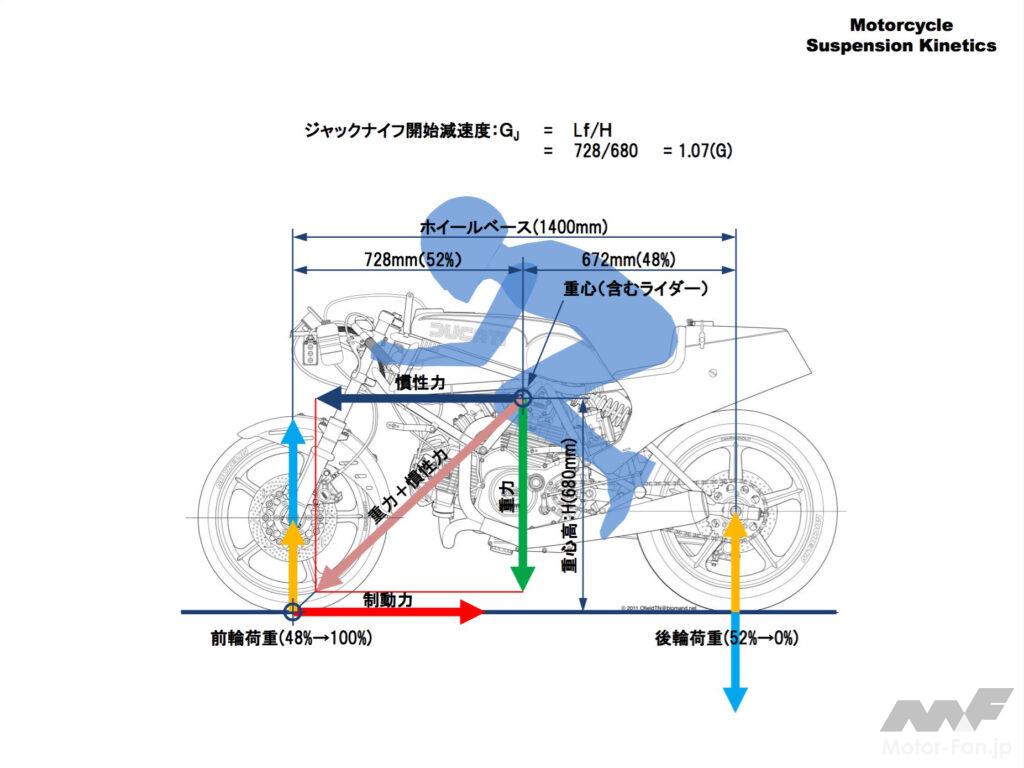
今度は定常走行の状態からブレーキをかけてみましょう。
制動すると前後輪の接地点に減速力が加えられ、重心には逆向きの「慣性力」(物体がそこに留まろうとする力)がはたらきます。
減速度をどんどん大きくしていくと後輪荷重はどんどん減少し、ついにゼロになります。
後輪荷重がゼロになると後輪ブレーキは効かないので、100%前輪でブレーキをかけることになります。
この状態から更に減速度を上げると後輪が持ち上がり前に転倒します。
この状態をジャックナイフと呼びます。
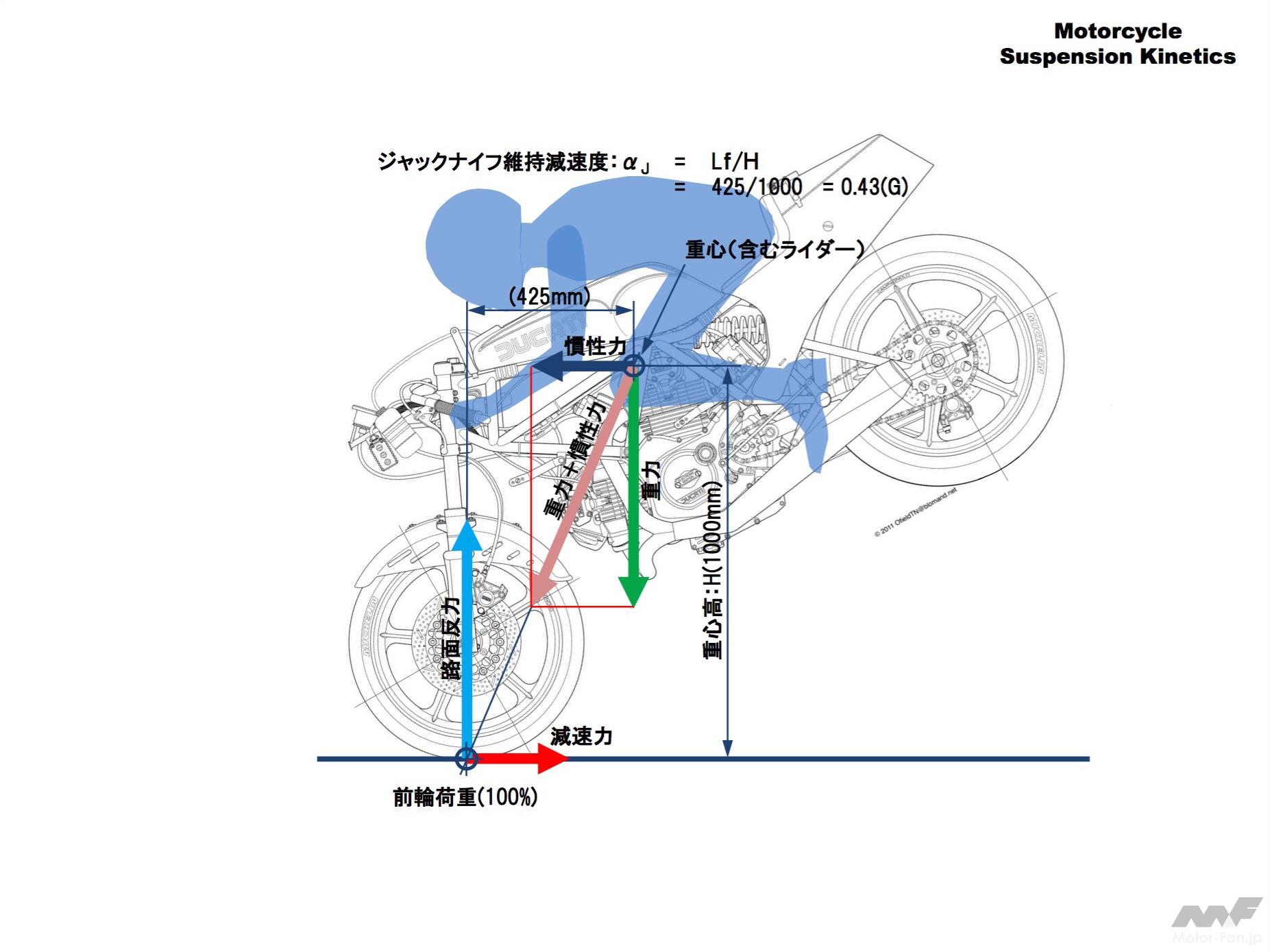
この状態は重力と慣性力の合力ベクトル(ピンクの矢印)の方向が前輪接地点を向いているということです。これからわかるようにジャックナイフ開始加速度が低い(簡単にジャックナイフしてしまう)条件は重心が高く、また前方にあることです。
これもあたりまえですがウィリーしやすい条件は重心が高いのは同じですが、前後位置は逆になります。
ジャックナイフが始まる減速度を「ジャックナイフ開始減速度(Gj)」とすると次の式で計算することができます。
ジャックナイフ開始減速度(Gj)=前輪から重心までの水平距離(mm)÷重心高(mm)
ジャックナイフの維持はむつかしい
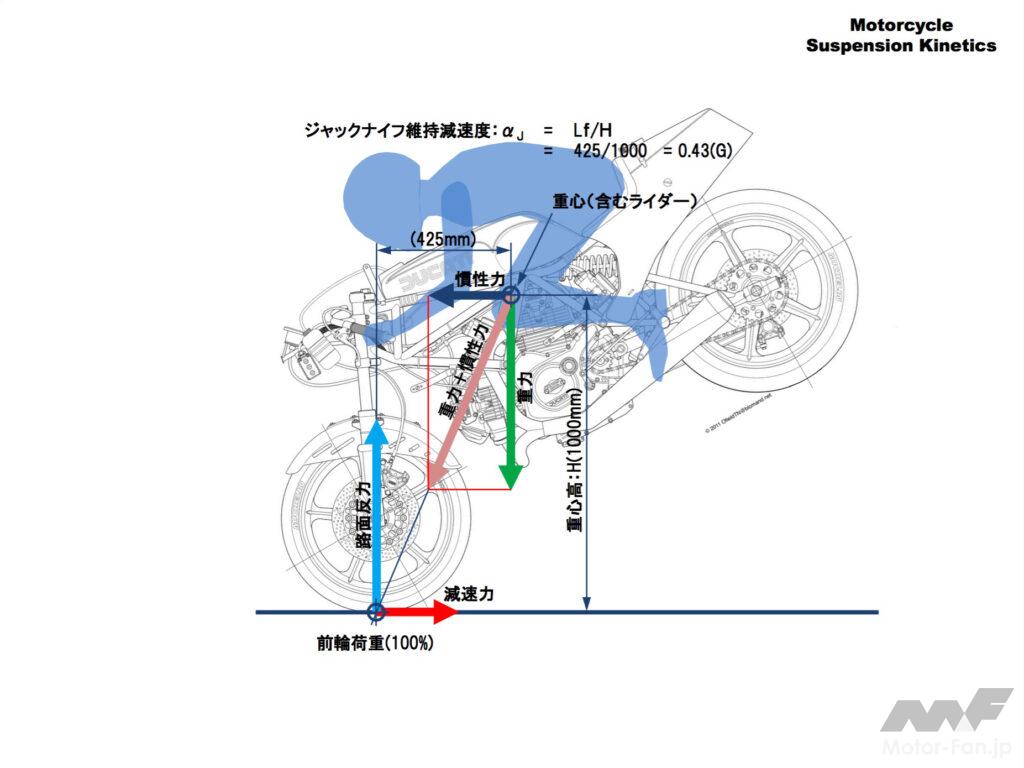
ブレーキを強くかけると前転してしまうのでゆるめ側のコントロールが必要です。
一旦後輪が持ち上がると更に重心高が上がりまた前輪から重心までの距離も小さくなるので上記のジャックナイフ維持減速度は小さくなります。
駆動力と制動力でコントロールできるウィリーと異なりジャックナイフ状態では前輪のブレーキだけでコントロールしなくてはならないのでジャックナイフ状態の維持は限定的です。

![by Motor-FanTECH.[モーターファンテック]](https://motor-fan.jp/wp-content/uploads/2025/04/mf-tech-logo.png)